Rearranging and Filtering Binned Data

Introduction

Event filtering refers to the process of removing or extracting a subset of events based on some criterion such as the temperature of the measured sample at the time an event was detected. Instead of extracting based on a single parameter value or interval, we may also want to rearrange data based on the parameter value, providing quick and convenient access to the parameter-dependence of our data. Scipp’s binned data can be used for both of these purposes.

The Quick Reference below provides a brief overview of the options. A more detailed walkthrough based on actual data can be found in the Full example.

Quick Reference

Extract events matching parameter value

Use label-based indexing on the bins property. This works similar to regular label-based indexing but operates on the unordered bin contents. Example:

param_value = sc.scalar(1.2, unit='m')
filtered = da.bins['param', param_value]

• The output data array has the same dimensions as the input da.

• filtered contains a copy of the filtered events.

Extract events falling into a parameter interval

Use label-based indexing on the bins property. This works similar to regular label-based indexing but operates on the unordered bin contents. Example:

start = sc.scalar(1.2, unit='m')
stop = sc.scalar(1.3, unit='m')
filtered = da.bins['param', start:stop]

• The output data array has the same dimensions as the input da. filtered contains a copy of the filtered events.

• Note that as usual the upper bound of the interval (here \(1.3~\text{m}\)) is not included.

Split into bins based on a discrete event parameter

Use scipp.group. Example:

split = da.group('param')

• The output data array has a new dimension 'param' in addition to the dimensions of the input.

• split contains a copy of the reordered events.

• Pass an explicit variable to group listing desired groups to limit what is included in the output.

Split into bins based on a continuous event parameter

Use scipp.bin. Example:

split = da.bin(param=10)

• The output data array has a new dimension 'param' in addition to the dimensions of the input.

• split contains a copy of the reordered events.

• Provide an explicit variable to bin to limit the parameter interval that is included in the output, or for fine-grained control over the sub-intervals.

Compute derived event parameters for subsequent extracting or splitting

Use scipp.transform_coords. Example:

da2 = da.transform_coords(derived_param=lambda p1, p2: p1 + p2)

da2 can now be used with any of the methods for extracting or splitting data described above. The intermediate variable can also be omitted, and we can directly extract or split the result:

filtered = da.transform_coords(derived_param=lambda p1, p2: p1 + p2) \
             .bin(derived_param=10)

Compute derived event parameters from time-series or other metadata

In practice, events are often tagged with a timestamp, which can be used to lookup parameter values from, e.g., a time-series log given by a data array with a single dimension and a coordinate matching the coordinate name of the timestamps. Use scipp.lookup with scipp.transform_coords. Example:

temperature = da.attrs['sample_temperature'].value  # temperature value time-series
interp_temperature = sc.lookup(temperature, mode='previous')
filtered = da.transform_coords(temperature=interp_temperature) \
             .bin(temperature=10)

Full example

Input data

In the following we use neutron diffraction data for a stainless steel tensile bar in a loadframe measured at the VULCAN Engineering Materials Diffractometer, kindly provided by the SNS. Scipp’s sample data includes an excerpt from the full dataset:

import scipp as sc

dg = sc.data.vulcan_steel_strain_data()
dg

Downloading file 'VULCAN_221040_processed.h5' from 'https://public.esss.dk/groups/scipp/scipp/2/VULCAN_221040_processed.h5' to '/home/runner/.cache/scipp/2'.

scipp.DataGroup

(dspacing: 100, time: None)

• data

  scipp

  DataArray

  (dspacing: 100)

  DataArrayView

  binned data [len=15467, len=14879, ..., len=1477, len=1318]
• loadframe.strain

  scipp

  DataArray

  (time: 5280)

  float64

  𝟙

  -0.000, -8.800e-05, ..., 0.639, 0.639
• proton_charge

  scipp

  DataArray

  (time: 234694)

  float64

  pC

  0.0, 2.344e+07, ..., 0.0, 2.332e+07

da = dg['data']
da

scipp.DataArray (77.45 MB)

• Dimensions:
  • dspacing: 100
• Coordinates: (1)
  • dspacing
    (dspacing [bin-edge])
    float64
    Å
    1.5, 1.51, ..., 2.49, 2.5

    Values:
    array([1.5 , 1.51, 1.52, 1.53, 1.54, 1.55, 1.56, 1.57, 1.58, 1.59, 1.6 ,
           1.61, 1.62, 1.63, 1.64, 1.65, 1.66, 1.67, 1.68, 1.69, 1.7 , 1.71,
           1.72, 1.73, 1.74, 1.75, 1.76, 1.77, 1.78, 1.79, 1.8 , 1.81, 1.82,
           1.83, 1.84, 1.85, 1.86, 1.87, 1.88, 1.89, 1.9 , 1.91, 1.92, 1.93,
           1.94, 1.95, 1.96, 1.97, 1.98, 1.99, 2.  , 2.01, 2.02, 2.03, 2.04,
           2.05, 2.06, 2.07, 2.08, 2.09, 2.1 , 2.11, 2.12, 2.13, 2.14, 2.15,
           2.16, 2.17, 2.18, 2.19, 2.2 , 2.21, 2.22, 2.23, 2.24, 2.25, 2.26,
           2.27, 2.28, 2.29, 2.3 , 2.31, 2.32, 2.33, 2.34, 2.35, 2.36, 2.37,
           2.38, 2.39, 2.4 , 2.41, 2.42, 2.43, 2.44, 2.45, 2.46, 2.47, 2.48,
           2.49, 2.5 ])

• Data: (1)
  • (dspacing)
    DataArrayView
    binned data [len=15467, len=14879, ..., len=1477, len=1318]

    dim='event',
    content=DataArray(
              dims=(event: 3383427),
              data=float32[counts],
              coords={'dspacing':float64[Å], 'time':datetime64[ns]})

The dspacing dimension is the interplanar lattice spacing (the spacing between planes in a crystal), and plotting this data we see two diffraction peaks:

da.hist().plot()

Extract time interval

The mechanical strain of the steel sample in the loadframe is recorded in the metadata:

strain = dg['loadframe.strain']
strain.plot()

We see that the strain drops off for some reason at the end. We can filter out those events, by extracting the rest as outlined in Extract events matching parameter value:

import numpy as np

start = strain.coords['time'][0]
stop = strain.coords['time'][np.argmax(strain.values)]
da = da.bins['time', start:stop]

Note

The above is just a concise way of binning into a single time interval and squeezing the time dimension from the result.

If multiple intervals are to be extracted then the mechanism based on start and stop values becomes highly inefficient, as every time da.bins['param', start:stop] is called all of the events have to be processed. Instead prefer using da.bin(param=param_bin_edges) and slice the result using regular positional (or label-based) indexing. Similarly, prefer using da.group('param') to extract based on multiple discrete values.

Filter bad pulses

In the previous example we directly used an existing event-coordinate (da.bins.coords['time']) for selecting the desired subset of data. In many practical cases such a coordinate may not be available yet and needs to be computed as a preparatory step. Scipp facilitates this using scipp.transform_coords and scipp.lookup. When the desired event-coordinate can be computed directly from existing coordinates then transform_coords can do the job on its own. In other cases, such as the following example, we combine it with lookup to, e.g., map timestamps to corresponding sensor readings.

Our data stores the so called proton charge, the total charge of protons per pulse (which produced the neutrons scattered off the sample):

proton_charge = dg['proton_charge']
proton_charge.plot()

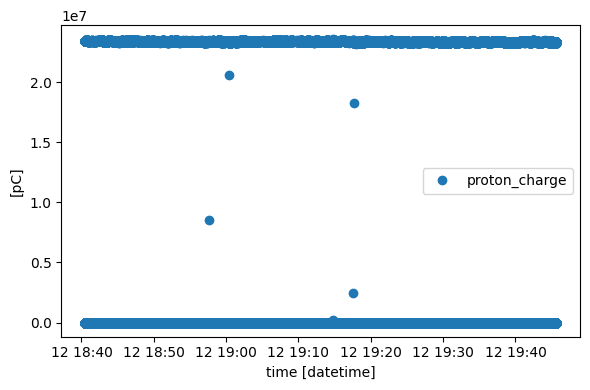
Some pulses have a very low proton charge which may indicate a problem with the source, so we may want to remove events that were produced from these pulses. We can use lookup to define the following “interpolation function”, marking any pulse as “good” if it has more than 90% of the mean proton charge:

good_pulse = sc.lookup(proton_charge > 0.9 * proton_charge.mean(), mode='previous')

transform_coords can utilize this interpolation function to compute a new coordinate (good_pulse, with True and False values) from the da.bins.coords['time'] coordinate. We used mode='previous' above, so an event’s good_pulse value will be defined by the previous pulse, i.e., the one that produced the neutron event. See the documentation of scipp.lookup for a full list of available options.

The return value of transform_coords can then be used to index the bins property, here to extract only the events that have good_pulse=True, i.e., were created by a proton pulse that fulfilled the above criterion:

da = da.transform_coords(good_pulse=good_pulse).bins['good_pulse', sc.index(True)]
da

scipp.DataArray (76.20 MB)

• Dimensions:
  • dspacing: 100
• Coordinates: (3)
  • dspacing
    (dspacing [bin-edge])
    float64
    Å
    1.5, 1.51, ..., 2.49, 2.5

    Values:
    array([1.5 , 1.51, 1.52, 1.53, 1.54, 1.55, 1.56, 1.57, 1.58, 1.59, 1.6 ,
           1.61, 1.62, 1.63, 1.64, 1.65, 1.66, 1.67, 1.68, 1.69, 1.7 , 1.71,
           1.72, 1.73, 1.74, 1.75, 1.76, 1.77, 1.78, 1.79, 1.8 , 1.81, 1.82,
           1.83, 1.84, 1.85, 1.86, 1.87, 1.88, 1.89, 1.9 , 1.91, 1.92, 1.93,
           1.94, 1.95, 1.96, 1.97, 1.98, 1.99, 2.  , 2.01, 2.02, 2.03, 2.04,
           2.05, 2.06, 2.07, 2.08, 2.09, 2.1 , 2.11, 2.12, 2.13, 2.14, 2.15,
           2.16, 2.17, 2.18, 2.19, 2.2 , 2.21, 2.22, 2.23, 2.24, 2.25, 2.26,
           2.27, 2.28, 2.29, 2.3 , 2.31, 2.32, 2.33, 2.34, 2.35, 2.36, 2.37,
           2.38, 2.39, 2.4 , 2.41, 2.42, 2.43, 2.44, 2.45, 2.46, 2.47, 2.48,
           2.49, 2.5 ])

  • good_pulse
    ()
    bool
    True

    Values:
    array(True)

  • time
    (time [bin-edge])
    datetime64
    ns
    2022-07-12T18:40:33.761038159, 2022-07-12T19:44:50.871666857

    Values:
    array(['2022-07-12T18:40:33.761038159', '2022-07-12T19:44:50.871666857'],
          dtype='datetime64[ns]')

• Data: (1)
  • (dspacing)
    DataArrayView
    binned data [len=15269, len=14701, ..., len=1450, len=1308]

    dim='event',
    content=DataArray(
              dims=(event: 3328840),
              data=float32[counts],
              coords={'dspacing':float64[Å], 'time':datetime64[ns]})

Rearrange data based on strain

As outlined in Split into bins based on a continuous event parameter we can rearrange data based on the current strain value at the time a neutron event was recorded:

interpolate_strain = sc.lookup(strain, mode='previous')
filtered = da.transform_coords(strain=interpolate_strain).bin(strain=100)

We can histogram and plot the result, but the figure is not very illuminating. This illustrates a common problem, and we will show below how to address it:

filtered.hist().transpose().plot()

The problem we run into with the above figure is that we have a lot more data (events) at zero strain than for the other strain values. We should therefore normalize the result to the incident flux. In this simplified example we can use the proton charge to accomplish this. We compute the integrated proton charge for a given strain value:

proton_charge = dg['proton_charge']
charge_per_time_interval = proton_charge.bin(time=strain.coords['time'])
charge_per_time_interval.coords['strain'] = strain.data
charge_per_strain_value = charge_per_time_interval.bin(
    strain=filtered.coords['strain']
).hist()

We can then normalize our data and obtain a more meaningful plot. It is now clearly visible how one of the diffraction peaks splits into two under increasing mechanical strain on the sample:

normalized = filtered / charge_per_strain_value
normalized.hist(strain=30, dspacing=300).plot()

As we have reordered our data by strain, data for a specific strain value can now be cheaply extracted using positional or label-based indexing. This returns a view of the events, i.e., not a copy:

normalized['strain', 80].hist(dspacing=400).plot()

In practice it can be useful to integrate strain ranges for comparison in a 1-D plot. Here we simply histogram with a coarser strain binning:

coarse = normalized.hist(strain=6, dspacing=200)
strains = [coarse['strain', sc.scalar(x)] for x in [0.0, 0.3, 0.6]]
lines = {f"strain={strain.coords['strain'].values}": strain for strain in strains}
sc.plot(lines, norm='log')