Monte-Carlo propagation of uncertainties

This guide introduces the mc sub package for propagation of uncertainties using Monte-Carlo.

Monte-Carlo (MC) can propagate uncertainties through most operations including non-differentiable ones and operations that introduce correlations. It does so by sampling new data from an input with uncertainties, performing the desired operation on each sample, and combining the results to compute, e.g., a mean and variance. While this method is powerful, it is very expensive and in practice only applicable to relatively small and well behaved data.

Mathematically, the mc package does the following (the examples below will make the terminology more concrete).

Given a measured, empirical distribution of random variables \(\mathbf{X}\), we want to compute some parameter \(\theta\) (the result of our operation). We estimate \(\theta\) using an estimator \(s\), such that \(\hat{\theta} = s(\mathbf{X})\). We assume all \(X_i\) to be independently distributed with distribution \(X_i = P(\mu_i, \sigma_i)\), where \(\mu_i\) and \(\sigma_i\) are the mean and standard deviation of \(X_i\). We draw \(R\) samples (‘replicas’) from \(P\):

\[\mathbf{x}^\ast = [x_{i_1}^\ast,\, \dots, x_{i_n}^\ast], \quad \text{where} \quad x_i^\ast \sim X_i = P(\mu_i, \sigma_i).\]

Then we pass each sample to the estimator \(s\) to obtain replicas of the target parameter \(\hat{\theta}^\ast = s(\mathbf{x}^\ast)\). The final results are then, typically, the mean and variance over all \(R\) replicas

\[\begin{split}\mu(\hat{\theta}^\ast) = \frac{1}{R} \sum_{r=1}^{R}\,s(\mathbf{x}^\ast_r),\\\\ \text{var}(\hat{\theta}^\ast) = \frac{1}{R-1} \sum_{r=1}^{R}\,{\big(s(\mathbf{x}^\ast_r) - \mu(\hat{\theta}^\ast)\big)}^2\end{split}\]

Let’s look at some examples to make this more concrete. Suppose we are given some positions and time information and want to compute the corresponding speeds. We will assume that all input data is independently normally distributed. First, generate some dummy data of positions with uncertainties:

import matplotlib.pyplot as plt
import numpy as np
import plopp as pp
import scipp as sc

from scippuncertainty import mc

%matplotlib inline
plt.ioff()

# Format units of variances nicely.
sc.units.aliases['m^2/s^2'] = 'm^2/s^2'

rng = np.random.default_rng(381)
n = 10
x = sc.linspace("x", 1, 2, n)
variances = rng.uniform(0.01, 0.05, n) ** 2
pos = sc.DataArray(
    sc.array(
        dims=["x"],
        values=x.values + rng.normal(4.0, np.sqrt(variances)),
        variances=variances,
        unit="m",
    ),
    coords={"x": x},
)
pp.plot(pos)

One input variable

Suppose we want to compute some speed from the positions given above and the following time. For now, the time is assumed to be exact, i.e., it has no variances.

time = sc.DataArray(sc.scalar(10.0, unit="s"))

Define a function to compute the speed. This corresponds to the estimator \(s\). (You will see below why this returns a dict.)

def compute_speed(pos: sc.DataArray, time: sc.DataArray) -> dict[str, sc.DataArray]:
    return {"speed": pos / time}

Given these times and speed calculation, we could do regular error propagation using Scipp’s builtin mechanism. We can use this to check our MC results later.

speed_regular = compute_speed(pos=pos, time=time)["speed"]

Now, in order to compute the uncertainties with MC, we need to create a few helper objects. First, define a sampler. This will be used to draw new samples from the input pos. Since we assume normally distributed data, we use a NormalDenseSampler. This defines the distribution \(X_i = P(\mu_i, \sigma_i)\).

pos_sampler = mc.NormalDenseSampler(pos)

Next, we need to define how to collect the replicas and compute an output statistic. In this case, we simply want to compute the mean and variance which is implemented by VarianceAccum.

accumulator = mc.VarianceAccum()

Finally, we can use mc.run to put everything together and actually perform the MC computation.

We pass a dict as the samplers that identifies the pos_sampler with the pos argument of compute_speed. The accumulators dict defines how to accumulate each output of compute_speed. There is only one here, but the accumulators still have to match the name in the dict returned by compute_speed. Since time has no uncertainties, we simply bind our fixed values using partial.

n_samples corresponds to the number of replicas \(R\). It is very high in this case because the computation is quite fast. In practice, numbers in the hundreds or low thousands are more feasible. Lastly, we disable progress reporting as this does not work reliably in Jupyter.

from functools import partial

results = mc.run(
    partial(compute_speed, time=time),
    samplers={"pos": pos_sampler},
    accumulators={"speed": accumulator},
    n_samples=10_000,
    progress=False,
)
speed_mc = results["speed"]

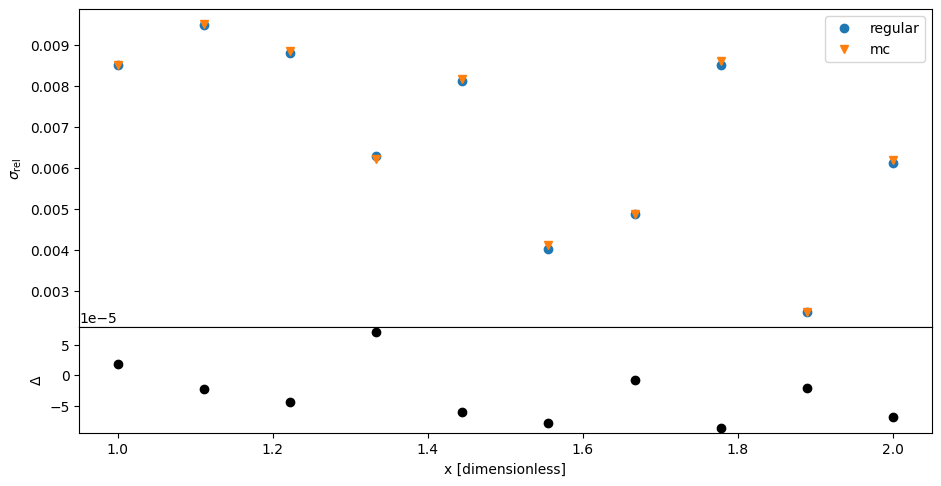
Now compare the results of the two calculations. It looks like MC and ‘regular’ uncertainty propagation are in agreement.

pp.plot({"regular": speed_regular, "mc": speed_mc}, ls='-', marker=None)

Also compare the relative errors of both results. Again, there is general agreement as expected. However there are some deviations because MC has only a finite precision.

Attention

Always make sure that your MC has properly converged to the desired precision. See the choosing \(R\) section below.

def relative_error(da: sc.DataArray) -> sc.DataArray:
    return sc.stddevs(da) / abs(sc.values(da))

def plot_relative_errors(
    data_regular: sc.DataArray, data_mc: sc.DataArray
) -> sc.DataArray:
    rel_err_regular = relative_error(data_regular)
    rel_err_mc = relative_error(data_mc)

    fig = plt.figure(figsize=(11, 5.5))
    gs = fig.add_gridspec(2, 1, height_ratios=(3, 1), hspace=0)

    ax = fig.add_subplot(gs[0])
    pp.plot({"regular": rel_err_regular, "mc": rel_err_mc}, ax=ax)
    ax.set_ylabel(r"$\sigma_\mathsf{rel}$")

    ax = fig.add_subplot(gs[1])
    pp.plot(rel_err_regular - rel_err_mc, ax=ax, c="k")
    ax.set_ylabel(r"$\Delta$")

    return fig

plot_relative_errors(speed_regular, speed_mc)

Broadcasting: introduction of correlations

This section introduces both the impact of correlations and how to sample from multiple inputs.

In the section above, there is no reason to use Monte-Carlo to propagate uncertainties because Scipp’s builtin method is correct. So now, let us look at a case where regular uncertainty propagation fails because it cannot account for correlations. A common source of correlations in Scipp is broadcasting of data with variances. To this end, define a new time data array, this time with variances:

time_with_var = sc.DataArray(sc.scalar(10.0, variance=0.1**2, unit="s"))

Modify the speed function to also compute the average speed as this is sensitive to correlations:

def compute_average_speed(
    pos: sc.DataArray, time: sc.DataArray
) -> dict[str, sc.DataArray]:
    speed = pos / time
    return {"speed": speed, "average_speed": sc.mean(speed)}

Trying to call compute_average_speed with this new time raises an exception. This is because time needs to be broadcast to match the shape of pos. In other words, the same time value needs to be divided into every single position value. This would introduce correlations between the resulting speeds as they would all depend on the same time and its uncertainty. Scipp cautiously prevents such broadcasts.

compute_average_speed(pos=pos, time=time_with_var)

---------------------------------------------------------------------------
VariancesError                            Traceback (most recent call last)
Cell In[15], line 1
----> 1 compute_average_speed(pos=pos, time=time_with_var)

Cell In[14], line 4, in compute_average_speed(pos, time)
      1 def compute_average_speed(
      2     pos: sc.DataArray, time: sc.DataArray
      3 ) -> dict[str, sc.DataArray]:
----> 4     speed = pos / time
      5     return {"speed": speed, "average_speed": sc.mean(speed)}

VariancesError: Cannot broadcast object with variances as this would introduce unhandled correlations. Input dimensions were:
(x: 10) variances=True
() variances=True

See https://doi.org/10.3233/JNR-220049 for more background.

For this guide, let us bypass Scipp’s check by using an explicit broadcast.

Warning

In practice, you have to check whether this is valid for your concrete use case!

results = compute_average_speed(
    pos=pos, time=sc.broadcast(time_with_var, sizes=pos.sizes).copy()
)
speed_regular = results["speed"]
average_speed_regular = results["average_speed"]

Now, set up the MC run in a similar way to before. First, define samplers for both position and time. This defines the probability distribution as the concatenation \(X = [P_{\text{pos}}(\mu, \sigma), P_{\text{time}}(\mu, \sigma)]\).

pos_sampler = mc.NormalDenseSampler(pos)
time_sampler = mc.NormalDenseSampler(time_with_var)

Define accumulators for both outputs of compute_average_speed:

speed_accumulator = mc.VarianceAccum()
average_speed_accumulator = mc.VarianceAccum()

And then perform the MC computation:

results = mc.run(
    compute_average_speed,
    samplers={"pos": pos_sampler, "time": time_sampler},
    accumulators={
        "speed": speed_accumulator,
        "average_speed": average_speed_accumulator,
    },
    n_samples=10_000,
    progress=False,
)
speed_mc = results["speed"]
average_speed_mc = results["average_speed"]

We can inspect the relative error of the speed per position as before. Again, MC and regular uncertainty propagation mostly agree. (The larger discrepancies compared to before are due to the larger spread of samples in MC due to the variance of time).

plot_relative_errors(speed_regular, speed_mc)

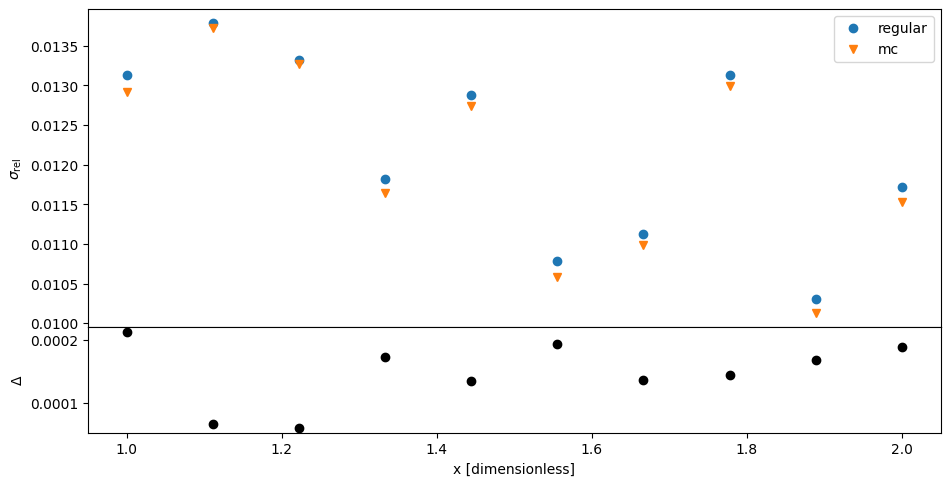
The above is expected because the induced correlations do not show up in the variances of the speed. We need to look at a quantity that is sensitive to those correlations. For example, the average speed as it is summed over all component speeds.

Indeed, MC produces a significantly larger standard deviation than regular propagation of uncertainties:

print(f"Regular: {average_speed_regular.data:c}")
print(f"MC:      {average_speed_mc.data:c}")

Regular: 0.549(2) m/s
MC:      0.549(6) m/s

Computing the covariance matrix

We can also compute the covariance matrix directly. This lets us inspect correlations of the results on more general grounds.

Again, define samplers for position and time:

pos_sampler = mc.NormalDenseSampler(pos)
time_sampler = mc.NormalDenseSampler(time_with_var)

Then, define an accumulator for the covariance in addition to the variance.

Note that Scipp has no native way of encoding matrices. So we work around this by storing a 2D array with artificial dimension labels (dims).

variance_accumulator = mc.VarianceAccum()
covariance_accumulator = mc.CovarianceAccum(dims=("x0", "x1"))

In order to use this, we need to return an additional result from our speed function. Since we want both the mean+variance and covariance matrix of the same result, the speed, we simply return it twice.

def compute_speed_cov(pos: sc.DataArray, time: sc.DataArray) -> dict[str, sc.DataArray]:
    speed = pos / time
    return {"speed": speed, "speed_cov": speed}

Now, run the MC calculation:

results = mc.run(
    compute_speed_cov,
    samplers={"pos": pos_sampler, "time": time_sampler},
    accumulators={"speed": variance_accumulator, "speed_cov": covariance_accumulator},
    n_samples=10_000,
    progress=False,
)
speed_mc = results["speed"]
speed_cov = results["speed_cov"]

speed_mc is the same as before. And speed_cov holds the variance-covariance matrix:

pp.plot(speed_cov)

The variance-covariance matrix is difficult to interpret. So compute the linear correlation matrix:

from scippuncertainty import pearson_correlation

pp.plot(pearson_correlation(speed_cov), vmin=0.0, vmax=1.0)

We can see that there are significant correlations between speeds, characterized by off-diagonal elements being close to 1.

Notes

Caveats

Monte-Carlo is a big gun and should only be used as a last resort. It requires large computational resources, time and memory. So much so that a supercomputer is required for many non-trivial problems. It is generally advisable to look for different solutions. It may, for example, be possible to compute variance-covariance matrices analytically or use an automatic differentiation library.

Monte-Carlo is a random process and as such only produces estimates of uncertainties. And the uncertainty of those estimates usually reduces as \(1 / \sqrt{R}\). This makes MC prohibitively expensive if the estimated distribution has a wide spread. For the examples above, if the input variables for position and time had standard deviations larger than a few percent, the MC results would be too noisy to be useful.

Choosing \(R\)

\(R\) needs to be large enough for MC to converge. Empirically, convergence can be determined by running MC with a given \(R\), say 100, and store the result. Then, run it again with a larger \(R\), say 1000, and check if there is a significant difference in the results.

Anecdotally, an \(R\) in the hundreds is often sufficient. However, as mentioned above, MC converges rather slowly as \(1 / \sqrt{R}\). So some cases will require much larger \(R\)s.

Random number generators and seeding

By default, mc.run constructs its own random number generator (RNG) and seeds it from the system RNG. If you want to make the process reproducible, you can pass a concrete seed via the seed argument. See the documentation of mc.run for details.

mc.run also sends a log message with the seed it uses. We can see it by configuring the logger, e.g., using the following.

import logging
from scippuncertainty.logging import get_logger

handler = logging.StreamHandler()
handler.setLevel("INFO")
get_logger().addHandler(handler)
get_logger().setLevel("INFO")

results = mc.run(
    compute_average_speed,
    samplers={"pos": pos_sampler, "time": time_sampler},
    accumulators={
        "speed": speed_accumulator,
        "average_speed": average_speed_accumulator,
    },
    n_samples=10,
    progress=False,
)

Seeding 1 random generators with entropy 186879802730428864953925297439487444399.
The generators are of type Generator(PCG64) from numpy.random version 1.26.4

Multi-threading

mc.run can use multiple threads where each thread processes a subset of samples. Simply set the desired number of threads with the n_threads argument.

But bear in mind that this uses Python’s threads. So you will only see a speedup if your function spends a lot of time in code that releases the global interpreter lock (GIL). Most functions in Scipp do this. However, since the data in the examples here is so small, multi threading does not improve performance.

Note further that most functions in Scipp are internally multi threaded. So you should make sure not to oversubscribe your CPU.

Skipping samples

Monte-Carlo can sometimes produce samples that our operation cannot handle, for example because a sample contains a 0 or a fit fails to converge. It is possible to skip those samples.

For example, suppose that we had a function that requires positive inputs like sqrt. We can detect negative inputs and return mc.SkipSample instead of actual data. This instructs mc.run to ignore this sample and carry on with the next one.

def skipping_op(da: sc.DataArray) -> dict[str, sc.DataArray]:
    if sc.any(da < sc.scalar(0)).value:
        return mc.SkipSample
    return {"sqrt": sc.sqrt(da)}

Note, though, that failed samples still count towards the target n_samples passed to mc.run. So the actual number of samples used for the output variance can be different. To find out, look at the n_samples' property:

# Data with large variances s.t. some samples are negative.
n = 10
x = sc.linspace("x", 1, 2, n)
da = sc.DataArray(
    sc.array(
        dims=["x"],
        values=x.values,
        variances=rng.uniform(0.1, 1.0, n) ** 2,
    ),
    coords={"x": x},
)

results = mc.run(
    skipping_op,
    samplers={"da": mc.NormalDenseSampler(da)},
    accumulators={"sqrt": mc.VarianceAccum()},
    n_samples=100,
    progress=False,
)
results.n_samples

Seeding 1 random generators with entropy 324519139704576124022978518398527001200.
The generators are of type Generator(PCG64) from numpy.random version 1.26.4

80