scipp.interpolate.interp1d
scipp.interpolate.interp1d#
- scipp.interpolate.interp1d(da, dim, *, kind='linear', fill_value=nan, **kwargs)#
Interpolate a 1-D function.
A data array is used to approximate some function f: y = f(x), where y is given by the array values and x is is given by the coordinate for the given dimension. This class returns a function whose call method uses interpolation to find the value of new points.
The function is a wrapper for scipy.interpolate.interp1d. The differences are:
Instead of x and y, a data array defining these is used as input.
Instead of an axis, a dimension label defines the interpolation dimension.
The returned function does not just return the values of f(x) but a new data array with values defined as f(x) and x as a coordinate for the interpolation dimension.
The returned function accepts an extra argument
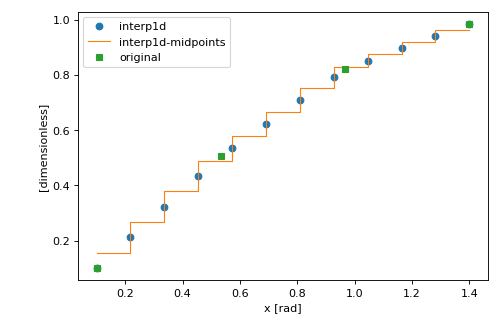
midpoints. When settingmidpoints=Truethe interpolation uses the midpoints of the new points instead of the points itself. The returned data array is then a histogram, i.e., the new coordinate is a bin-edge coordinate.
If the input data array contains masks that depend on the interpolation dimension the masked points are treated as missing, i.e., they are ignored for the definition of the interpolation function. If such a mask also depends on additional dimensions
scipp.DimensionErroris raised since interpolation requires points to be 1-D.For structured input data dtypes such as vectors, rotations, or linear transformations interpolation is structure-element-wise. While this is appropriate for vectors, such a naive interpolation for, e.g., rotations does typically not yield a rotation so this should be used with care, unless the ‘kind’ parameter is set to, e.g., ‘previous’, ‘next’, or ‘nearest’.
Parameters not described above are forwarded to scipy.interpolate.interp1d. The most relevant ones are (see
scipy.interpolate.interp1dfor details):- Parameters
da (
DataArray) – Input data. Defines both dependent and independent variables for interpolation.dim (
str) – Dimension of the interpolation.kind (
Union[int,Literal[‘linear’, ‘nearest’, ‘nearest-up’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’, ‘previous’, ‘next’]], default:'linear') –integer: order of the spline interpolator
string:
’zero’, ‘slinear’, ‘quadratic’, ‘cubic’: spline interpolation of zeroth, first, second or third order
’previous’ and ‘next’: simply return the previous or next value of the point
’nearest-up’ and ‘nearest’ differ when interpolating half-integers (e.g. 0.5, 1.5) in that ‘nearest-up’ rounds up and ‘nearest’ rounds down
fill_value (
Any, default:nan) – Set to ‘extrapolate’ to allow for extrapolation of points outside the range.
- Returns
Callable– A callablef(x)that returns interpolated values ofdaatx.
Examples
>>> x = sc.linspace(dim='x', start=0.1, stop=1.4, num=4, unit='rad') >>> da = sc.DataArray(sc.sin(x), coords={'x': x})
>>> from scipp.interpolate import interp1d >>> f = interp1d(da, 'x')
>>> xnew = sc.linspace(dim='x', start=0.1, stop=1.4, num=12, unit='rad') >>> f(xnew) # use interpolation function returned by `interp1d` <scipp.DataArray> Dimensions: Sizes[x:12, ] Coordinates: x float64 [rad] (x) [0.1, 0.218182, ..., 1.28182, 1.4] Data: float64 [dimensionless] (x) [0.0998334, 0.211262, ..., 0.941144, 0.98545]
>>> f(xnew, midpoints=True) <scipp.DataArray> Dimensions: Sizes[x:11, ] Coordinates: x float64 [rad] (x [bin-edge]) [0.1, 0.218182, ..., 1.28182, 1.4] Data: float64 [dimensionless] (x) [0.155548, 0.266977, ..., 0.918992, 0.963297]
>>> sc.plot({'original':da, ... 'interp1d':f(xnew), ... 'interp1d-midpoints':f(xnew, midpoints=True)})